The Maze

描述

There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the maze, the ball's start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return true if the ball can stop at the destination, otherwise return false.

You may assume that the borders of the maze are all walls (see examples).

Example 1:

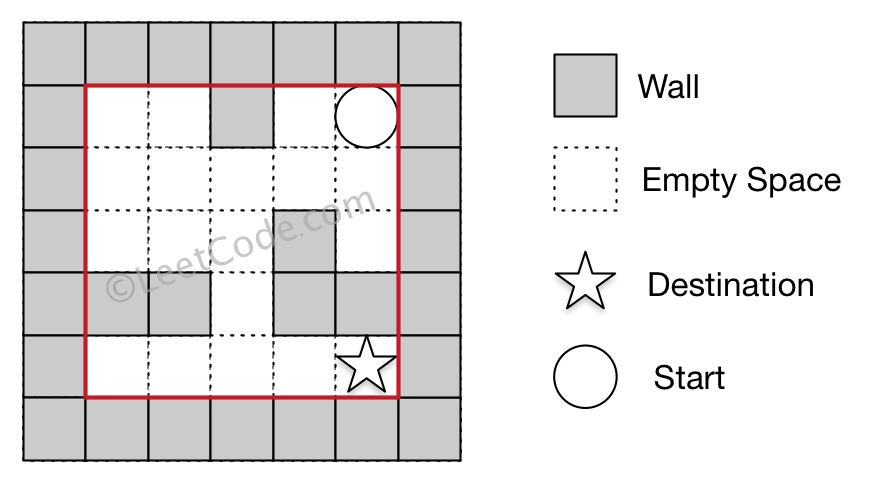
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

Example 2:

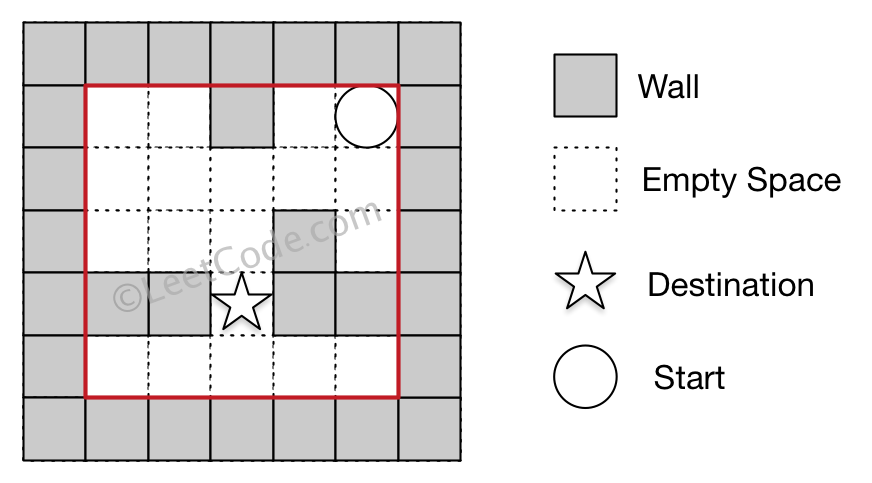
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
Output: false
Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.

Example 3:

Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
Output: false

Constraints:

• $1 \leq maze.length, maze[i].length \leq 100$
• maze[i][j] is 0 or 1.
• start.length == 2
• destination.length == 2
• 0 \leq $start_row, destination_row$ \leq maze.length
• 0 \leq $start_col, destination_col$ \leq maze[i].length
• Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
• The maze contains at least 2 empty spaces.

分析

只需要输出 true或者false, 用 DFS 和 BFS 都可以。

代码

DFS

Python

# The Maze
# DFS
# Time Complexity: O(mn), Space Complexity: O(mn)
class Solution:
    def hasPath(self, maze: List[List[int]], start: List[int], destination: List[int]) -> bool:
        m, n, visited = len(maze), len(maze[0]), set()
        def dfs(x, y):
            if (x, y) in visited:
                return False
            visited.add((x, y))
            if [x, y] == destination:
                return True
            for i, j in (-1, 0), (1, 0), (0, -1), (0, 1):
                newX, newY = x, y
                #  The ball won't stop rolling until hitting a wall
                while 0 <= newX + i < m and 0 <= newY + j < n and maze[newX + i][newY + j] != 1:
                    newX += i
                    newY += j
                if dfs(newX, newY):
                    return True
            return False

        return dfs(*start)

Java

// The Maze
// DFS
// Time Complexity: O(mn), Space Complexity: O(mn)
class Solution {
    public boolean hasPath(int[][] maze, int[] start, int[] destination) {
        int m = maze.length;
        int n = maze[0].length;
        boolean[][] visited = new boolean[m][n];
        return dfs(maze, destination, start, visited);
    }

    private boolean dfs(int[][] maze, int[] destination, int[] pos, boolean[][] visited) {
        int m = maze.length;
        int n = maze[0].length;
        if (visited[pos[0]][pos[1]]) return false;
        visited[pos[0]][pos[1]] = true;
        if (Arrays.equals(destination, pos)) return true;

        int[][] directions={{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        for(int[] direction : directions) {
            int i = direction[0], j = direction[1];
            int[] newPos = pos.clone();
            // The ball won't stop rolling until hitting a wall
            while(0 <= newPos[0]+i && newPos[0]+i < m && 0 <= newPos[1]+j && newPos[1]+j < n && maze[newPos[0] + i][newPos[1] + j] != 1) {
                newPos[0] += i;
                newPos[1] += j;
            }
            if (dfs(maze, destination, newPos, visited)) {
                return true;
            }
        }
        return false;
    }
}

C++

// The Maze
// DFS
// Time Complexity: O(mn), Space Complexity: O(mn)
class Solution {
public:
    bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
        int m = maze.size();
        int n = maze[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n));
        return dfs(maze, destination, start, visited);
    }

    bool dfs(const vector<vector<int>>& maze, const vector<int>& destination, const vector<int>& pos, vector<vector<bool>>& visited) {
        int m = maze.size();
        int n = maze[0].size();
        if (visited[pos[0]][pos[1]]) return false;
        visited[pos[0]][pos[1]] = true;
        if (destination == pos) return true;

        vector<vector<int>> directions={{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        for(const vector<int>& direction : directions) {
            int i = direction[0], j = direction[1];
            vector<int> newPos(pos);
            // The ball won't stop rolling until hitting a wall
            while(0 <= newPos[0]+i && newPos[0]+i < m && 0 <= newPos[1]+j && newPos[1]+j < n && maze[newPos[0] + i][newPos[1] + j] != 1) {
                newPos[0] += i;
                newPos[1] += j;
            }
            if (dfs(maze, destination, newPos, visited)) {
                return true;
            }
        }
        return false;
    }
};

BFS

Python

# The Maze
# BFS
# Time Complexity: O(mn), Space Complexity: O(mn)
class Solution:
    def hasPath(self, maze, start, destination):
        m = len(maze)
        n = len(maze[0])
        q = deque([start])

        # Do NOT use visited = [[False] * n] * m
        visited = [[False] * n for _ in range(m)]
        visited[start[0]][start[1]] = True

        while q:
            x, y = q.popleft()
            if [x, y] == destination: return True

            for i, j in (-1, 0), (1, 0), (0, -1), (0, 1):
                newX, newY = x, y
                #  The ball won't stop rolling until hitting a wall
                while 0 <= newX + i < m and 0 <= newY + j < n and maze[newX + i][newY + j] == 0:
                    newX += i
                    newY += j
                if not visited[newX][newY]:
                    q.append([newX, newY])
                    visited[newX][newY] = True

        return False

Java

TODO

C++

TODO

相关题目

• The Maze II
• The Maze III