The Maze II

描述

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball's start position, the destination and the maze, find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

Example 1:

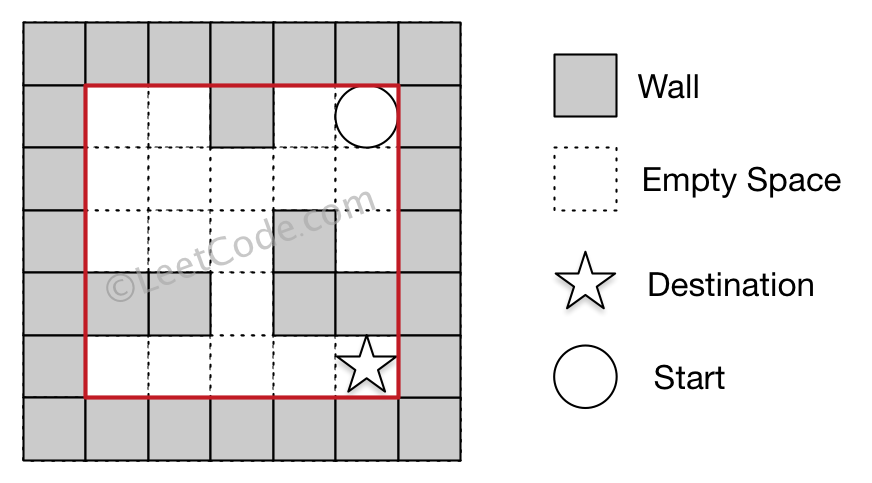
Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: 12

Explanation: One shortest way is : left -> down -> left -> down -> right -> down -> right.
The total distance is 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.

Example 2:

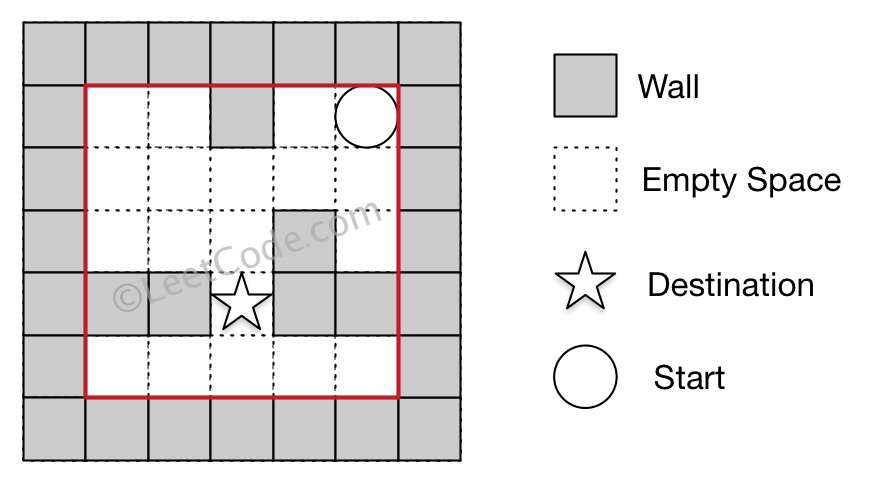
Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)

Output: -1

Explanation: There is no way for the ball to stop at the destination.

分析

求最短路径，很显然，用 BFS。通常判断重复用一个布尔二维矩阵visited即可，不过本题光这样判重是不够的，需要判断路径是否更短，因为本题一步不是单纯的只走一步，而是要一路碰到墙为止，所以用原始的BFS是不行的。

时间复杂度 $O(M \times N \times \max\left\{M, N\right\})$ , 因为要遍历每个位置，同时在每个位置要一直走到墙。空间复杂度 $O(M \times N)$，队列里最坏可能会存储所有的位置。

代码

Python

# TODO

Java

// The Maze II
// BFS
// Time complexity : O(m*n*max(m,n))
// Space complexity : O(mn)
public class Solution {
    public int shortestDistance(int[][] maze, int[] start, int[] dest) {
        final int M = maze.length, N = maze[0].length;
        int[][] distance = new int[M][N];
        for (int[] row: distance) Arrays.fill(row, Integer.MAX_VALUE);

        int[][] dirs={{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // up, down, left, right
        Queue<int[]> q = new LinkedList<>();

        distance[start[0]][start[1]] = 0;
        q.offer(start);
        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int x = cur[0], y = cur[1];

            for (int[] dir: dirs) {
                int newX = x, newY = y;
                int i = dir[0], j = dir[1];
                int step = distance[x][y];
                // walk until hit wall
                while (0 <= newX + i && newX + i < M && 0 <= newY + j && newY + j < N && maze[newX + i][newY + j] == 0) {
                    newX += i;
                    newY += j;
                    step++;
                }
                if (step < distance[newX][newY]) {
                    distance[newX][newY] = step;
                    q.offer(new int[] {newX, newY});
                }
            }
        }
        return distance[dest[0]][dest[1]] == Integer.MAX_VALUE ? -1 : distance[dest[0]][dest[1]];
    }
}

C++

TODO

相关题目

• The Maze
• The Maze III