LRU Cache

描述

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and set.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.

set(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

分析

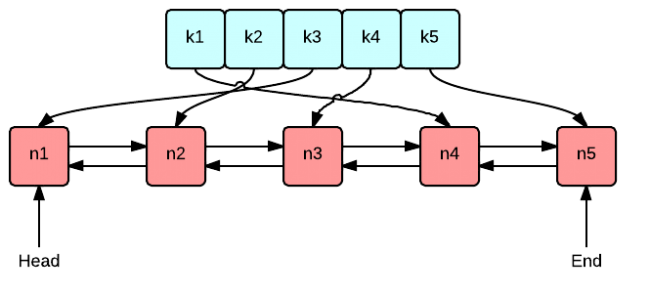
为了使查找、插入和删除都有较高的性能，这题的关键是要使用一个双向链表和一个 HashMap，因为：

• HashMap 保存每个节点的地址，可以基本保证在O(1)时间内查找节点
• 双向链表能后在O(1)时间内添加和删除节点，单链表则不行

具体实现细节：

• 越靠近链表头部，表示节点上次访问距离现在时间最短，尾部的节点表示最近访问最少
• 访问节点时，如果节点存在，把该节点交换到链表头部，同时更新 hash 表中该节点的地址
• 插入节点时，如果 cache 的 size 达到了上限 capacity，则删除尾部节点，同时要在 hash 表中删除对应的项；新节点插入链表头部

代码

C++的std::list 就是个双向链表，且它有个 splice()方法，O(1)时间，非常好用。

Java 中也有双向链表LinkedList, 但是 LinkedList 封装的太深，没有能在O(1)时间内删除中间某个元素的 API(C++的list有个splice(), O(1), 所以本题 C++可以放心使用splice())，于是我们只能自己实现一个双向链表。

本题有的人直接用 LinkedHashMap ，代码更短，但这是一种偷懒做法，面试官一定会让你自己重新实现。

Java

// LRU Cache
// HashMap + Doubly Linked List
public class LRUCache {
    private int capacity;
    private Map<Integer, DLinkedNode> m;
    private DLinkedList list;

    public LRUCache(int capacity) {
        this.capacity = capacity;
        m = new HashMap<>();
        list = new DLinkedList();
    }

    // Time Complexity: O(1)
    public int get(int key) {
        if (!m.containsKey(key)) return -1;
        DLinkedNode node = m.get(key);
        update(node);
        return node.value;
    }

    // Time Complexity: O(1)
    public void put(int key, int value) {
        if (m.containsKey(key)){
            DLinkedNode node = m.get(key);
            node.value = value;
            update(node);
        } else {
            DLinkedNode node = new DLinkedNode(key, value);
            if (m.size() >= capacity){
                DLinkedNode last = list.peekLast();
                m.remove(last.key);
                list.remove(last);
            }

            list.offerFirst(node);
            m.put(key, node);
        }
    }

    private void update(DLinkedNode node) {
        list.remove(node);
        list.offerFirst(node);
    }


    // Node of doubly linked list
    static class DLinkedNode {
        int key, value;
        DLinkedNode prev, next;

        DLinkedNode(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    // Doubly linked list
    static class DLinkedList {
        DLinkedNode head, tail;
        int size;

        DLinkedList() {
            // head and tail are two dummy nodes
            head = new DLinkedNode(0, 0);
            tail = new DLinkedNode(0, 0);
            head.next = tail;
            tail.prev = head;
        }

        // Add a new node at head
        void offerFirst(DLinkedNode node) {
            head.next.prev = node;
            node.next = head.next;
            node.prev = head;
            head.next = node;
            size++;
        }

        // Remove a node in the middle
        void remove(DLinkedNode node) {
            if (node == null) return;
            node.prev.next = node.next;
            node.next.prev = node.prev;
            size--;
        }

        DLinkedNode peekLast() {
            return tail.prev;
        }
    }
}

C++

// LRU Cache
class LRUCache{
private:
    // Node of doubly linked list
    class DLinkedNode {
    public:
        int key, value;
        DLinkedNode *prev=nullptr, *next=nullptr;

        DLinkedNode(int key, int value) {
            this->key = key;
            this->value = value;
        }
    };

    // Doubly linked list
    class DLinkedList {
    public:
        DLinkedList() {
            // head and tail are two dummy nodes
            head = new DLinkedNode(0, 0);
            tail = new DLinkedNode(0, 0);
            head->next = tail;
            tail->prev = head;
        }

        // Add a new node at head
        void offerFirst(DLinkedNode *node) {
            head->next->prev = node;
            node->next = head->next;
            node->prev = head;
            head->next = node;
            size++;
        }

        // Remove a node in the middle
        void remove(DLinkedNode *node) {
            if (node == nullptr) return;
            node->prev->next = node->next;
            node->next->prev = node->prev;
            size--;
        }

        DLinkedNode* peekLast() {
            return tail->prev;
        }
    private:
        DLinkedNode *head, *tail;
        int size;
    };

public:
    LRUCache(int capacity) {
        this->capacity = capacity;
    }

    // Time Complexity: O(1)
    int get(int key) {
        if (m.find(key) == m.end()) return -1;
        DLinkedNode *node = m[key];
        update(node);
        return node->value;
    }

    // Time Complexity: O(1)
    void put(int key, int value) {
        if (m.find(key) != m.end()){
            DLinkedNode *node = m[key];
            node->value = value;
            update(node);
        } else {
            DLinkedNode *node = new DLinkedNode(key, value);
            if (m.size() >= capacity){
                DLinkedNode *last = list.peekLast();
                m.erase(last->key);
                list.remove(last);
            }

            list.offerFirst(node);
            m[key] = node;
        }
    }

    void update(DLinkedNode *node) {
        list.remove(node);
        list.offerFirst(node);
    }
private:
    int capacity = 0;
    unordered_map<int, DLinkedNode*> m;
    DLinkedList list;
};

Python

# LRU Cache
# OrderedDict
class LRUCache:
    def __init__(self, capacity):
        self.capacity = capacity
        self.cache = OrderedDict()

    #  Time Complexity: O(1)
    def get(self, key):
        if key in self.cache:
            value = self.cache.pop(key)
            self.cache[key] = value
            return value
        else: return -1

    #  Time Complexity: O(1)
    def put(self, key, value):
        if key in self.cache:
            self.cache.pop(key)
        self.cache[key] = value
        if len(self.cache) > self.capacity:
            self.cache.popitem(last=False)

相关题目

• LFU Cache