Android Unlock Patterns

描述

Android devices have a special lock screen with a 3 x 3 grid of dots. Users can set an "unlock pattern" by connecting the dots in a specific sequence, forming a series of joined line segments where each segment's endpoints are two consecutive dots in the sequence. A sequence of k dots is a valid unlock pattern if both of the following are true:

• All the dots in the sequence are distinct.
• If the line segment connecting two consecutive dots in the sequence passes through any other dot, the other dot must have previously appeared in the sequence. No jumps through non-selected dots are allowed.

Here are some example valid and invalid unlock patterns:

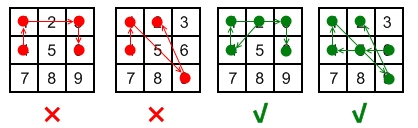
• The 1st pattern [4,1,3,6] is invalid because the line connecting dots 1 and 3 pass through dot 2, but dot 2 did not previously appear in the sequence.
• The 2nd pattern [4,1,9,2] is invalid because the line connecting dots 1 and 9 pass through dot 5, but dot 5 did not previously appear in the sequence.
• The 3rd pattern [2,4,1,3,6] is valid because it follows the conditions. The line connecting dots 1 and 3 meets the condition because dot 2 previously appeared in the sequence.
• The 4th pattern [6,5,4,1,9,2] is valid because it follows the conditions. The line connecting dots 1 and 9 meets the condition because dot 5 previously appeared in the sequence.

Given two integers m and n, return the number of unique and valid unlock patterns of the Android grid lock screen that consist of at least m keys and at most n keys.

Two unlock patterns are considered unique if there is a dot in one sequence that is not in the other, or the order of the dots is different.

Example 1:

Input: m = 1, n = 1
Output: 9

Example 2:

Input: m = 1, n = 2
Output: 65

Constraints:

• 1 <= m, n <= 9

分析

深搜，配合大量剪枝。

剪枝通常需要深入理解题意，掌握领域知识（domain knowledge）。本题有个比较重要的特性是，1,3,5,7 这 4 个点是互相对称的，即以 1 作为起点，得到的有效模式的个数，与以 3 作为起点，得到的有效模式的个数，是相等的，5, 7 也是类似。同理，2,4,6,8 这 4 个点也是对称的。

换句话说，令 f[i]表示以i为起点的有效模式的个数，总数就是 f[1]*4+f[2]*4+f[5]。

代码

Python

// Android Unlock Patterns
// Time Complexity O(n!), Space Complexity: O(n)
public class Solution {

    public int numberOfPatterns(int m, int n) {
        int[][] jumps = build_jump_table();
        boolean[] visited = new boolean[10];

        int count = 0;
        for(int i = m; i <= n; ++i) {
            count += dfs(visited, jumps, 1, i - 1) * 4;  // 1, 3, 7, 9 are symmetric
            count += dfs(visited, jumps, 2, i - 1) * 4;  // 2, 4, 6, 8 are symmetric
            count += dfs(visited, jumps, 5, i - 1);      // 5
        }
        return count;
    }

    private static int dfs(boolean visited[], int[][] jumps, int num, int remain) {
        if(remain == 0) return 1;

        int count = 0;
        visited[num] = true;
        for(int i = 1; i <= 9; ++i) {
            int mid = jumps[num][i]; // Edge num->i jumps over mid
            if(!visited[i] && (mid == 0 || (visited[mid]))) {
                count += dfs(visited, jumps, i, remain - 1);
            }
        }
        visited[num] = false;
        return count;
    }

    private int[][] build_jump_table() {
        int[][] jumps = new int[10][10]; // jump table, 0 means adjacent
        jumps[1][3] = jumps[3][1] = 2; // The edge 1->3 jumps over 2
        jumps[1][7] = jumps[7][1] = 4;
        jumps[3][9] = jumps[9][3] = 6;
        jumps[7][9] = jumps[9][7] = 8;
        jumps[2][8] = jumps[8][2] = jumps[4][6] = jumps[6][4] = 5;
        jumps[1][9] = jumps[9][1] = jumps[3][7] = jumps[7][3] = 5;
        return jumps;
    }
}

Java

// TODO

C++

# Android Unlock Patterns
# Time Complexity O(n!), Space Complexity: O(n)

def numberOfPatterns(m: int, n: int) -> int:
    def build_jump_table():
        jumps = [[0] * 10 for _ in range(10)]  # jump table, 0 means adjacent
        jumps[1][3] = jumps[3][1] = 2  # The edge 1->3 jumps over 2
        jumps[1][7] = jumps[7][1] = 4
        jumps[3][9] = jumps[9][3] = 6
        jumps[7][9] = jumps[9][7] = 8
        jumps[2][8] = jumps[8][2] = jumps[4][6] = jumps[6][4] = 5
        jumps[1][9] = jumps[9][1] = jumps[3][7] = jumps[7][3] = 5
        return jumps

    def dfs(visited, jumps, num, remain):
        if remain == 0:
            return 1

        count = 0
        visited[num] = True
        for i in range(1, 10):
            mid = jumps[num][i]  # Edge num->i jumps over mid
            if not visited[i] and (mid == 0 or visited[mid]):
                count += dfs(visited, jumps, i, remain - 1)
        visited[num] = False
        return count

    jumps = build_jump_table()
    visited = [False] * 10

    count = 0
    for i in range(m, n + 1):
        count += dfs(visited, jumps, 1, i - 1) * 4  # 1, 3, 7, 9 are symmetric
        count += dfs(visited, jumps, 2, i - 1) * 4  # 2, 4, 6, 8 are symmetric
        count += dfs(visited, jumps, 5, i - 1)      # 5
    return count